iopalarm.blogg.se - Simple linear regression excel

#Simple linear regression excel series#

This coefficient is only calculated if the constant of the model has not been fixed by the user. The adjusted R² can be negative if the R² is near to zero.

Adjusted R²: The adjusted determination coefficient for the model.

The problem with the R² is that it does not take into account the number of variables used to fit the model. The nearer R² is to 1, the better is the model. The R² is interpreted as the proportion of the variability of the dependent variable explained by the model. This coefficient, whose value is between 0 and 1, is only displayed if the constant of the model has not been fixed by the user.

R²: The determination coefficient for the model.

DF: The number of degrees of freedom for the chosen model (corresponding to the error part).

In the formulas shown below, W is the sum of the weights.

Sum of weights: The sum of the weights of the observations used in the calculations.

In the formulas shown below, n is the number of observations.

Observations: The number of observations used in the calculations.

Goodness of fit statistics:The statistics relating to the fitting of the regression model are shown in this table:.

Where the best model for a number of variables varying from p to q has been selected, the best model for each number or variables is displayed with the corresponding statistics and the best model for the criterion chosen is displayed in bold. For a stepwise selection, the statistics corresponding to the different steps are displayed.

Summary of the variables selection: Where a selection method has been chosen, XLSTAT displays the selection summary.

Homoscedasticity and independence of the error terms are key hypotheses in linear regression where it is assumed that the variances of the error terms are independent and identically distributed and normally distributed. XLSTAT allows to correct for heteroscedasticity and autocorrelation that can arise using several methods such as the estimator suggested by Newey and West (1987). Correcting for Heteroscedasticity and Autocorrelation

#Simple linear regression excel series#

The independence of the residuals can be checked by analyzing certain charts or by using the Durbin-Watson test (under Time Series menu). For this, you need to activate the respective test in the Test assumptions sub-tab. The normality of the residuals can be checked by analyzing certain charts or by running a Shapiro- Wilk test on the residuals. Use the various tests proposed in the results of linear regression to check retrospectively that the underlying hypotheses have been correctly verified. Validation of the hypothesis of linear regression The variables are then removed from the model following the procedure used for stepwise selection. Backward: The procedure starts by simultaneously adding all variables.Forward: The procedure is the same as for stepwise selection except that variables are only added and never removed.The procedure continues until no more variables can be added or removed. If the probability is greater than the "Probability of removal", the variable is removed.

After the third variable is added, the impact of removing each variable present in the model after it has been added is evaluated (still using the t statistic). If a second variable is such that the probability associated with its t is less than the "Probability for entry", it is added to the model.

Stepwise: The selection process starts by adding the variable with the largest contribution to the model (the criterion used is Student's t statistic).

Furthermore, the user can choose several "criteria" to determine the best model: Adjusted R², Mean Square of Errors (MSE), Mallows Cp, Akaike's AIC, Schwarz's SBC, Amemiya's PC.

Best model: This method lets you choose the best model from amongst all the models which can handle a number of variables varying from "Min variables" to "Max Variables".

It is possible to select the variables that are part of the model using one of the four available methods in XLSTAT: The linear regression hypotheses are that the errors e i follow the same normal distribution N(0,s) and are independent. The model is found by using the least squares method (the sum of squared errors e i² is minimized). Where y i is the value observed for the dependent variable for observation i, x ki is the value taken by variable k for observation i, and e i is the error of the model. The determinist is written for observation i as follows: The principle of linear regression is to model a quantitative dependent variable Y through a linear combination of p quantitative explanatory variables, X 1, X 2, …, X p.

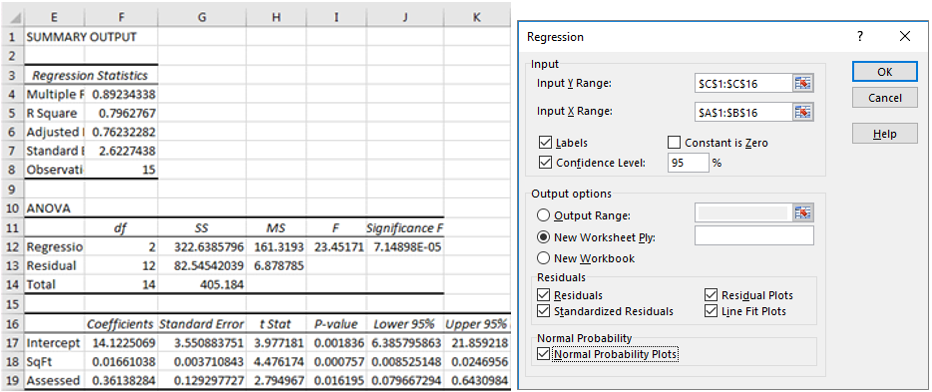
A distinction is usually made between simple regression (with only one explanatory variable) and multiple regression (several explanatory variables) although the overall concept and calculation methods are identical. Linear regression is, without doubt, one of the most frequently used statistical modeling methods.